SPSS方差分析
一、介绍
方差分析(ANOVA, Analysis of Variance)用于比较两个及以上组别的均值差异是否具有统计学显著性,核心思想是将“组间差异”和“组内差异”进行分解,通过 F 检验评估自变量(因素)对因变量的影响是否显著。
在 SPSS 软件中,方差分析主要用于样本量估算与检验效能(Power)评估:给定显著性水平(α)、期望检验效能(1-β)、效应量(Effect Size)以及组数与设计结构,计算每组所需样本数或在既定样本数下的检验效能。常见模块包括:
- Means - One-Way ANOVA(单因素方差分析)
- Means - Factorial ANOVA(多因素/析因方差分析)
- Means - Repeated Measures ANOVA(重复测量方差分析)
方差分析常用的前提假设:
- 独立性:各观测值相互独立。
- 正态性:各组因变量近似服从正态分布(或样本量足够大时中心极限定理近似满足)。
- 方差齐性:各组的方差近似相等(可用 Levene 检验等进行验证)。
在 SPSS 中进行样本量/效能分析的一般流程:
- 选择合适的 ANOVA 模块(如单因素、重复测量或析因设计)。
- 设置研究设计参数:组数、是否平衡设计(各组样本量相同)、均值方案或效应量、组内标准差或方差、α(常用 0.05)、目标 Power(常用 0.80 或 0.90)。
- 运行计算,查看每组所需样本量、总样本量或得到的检验效能,并据此调整设计。
二、单因素方差分析
2.1 准备数据
这里我们使用课本上的示例数据:《实验设计与数据分析—李云雁(第三版)》-P91
| 温度(℃) | 得率1 | 得率2 | 得率3 |
|---|---|---|---|
| 60 | 90 | 92 | 88 |
| 65 | 97 | 93 | 92 |
| 70 | 96 | 96 | 93 |
| 75 | 84 | 83 | 88 |
| 80 | 84 | 86 | 82 |
- 因素:温度(Temperature)
- 水平:5 个(60、65、70、75、80)
- 重复次数:3 次
- 响应变量:得率(Yield)
2.2 输入数据到SPSS
定义变量:
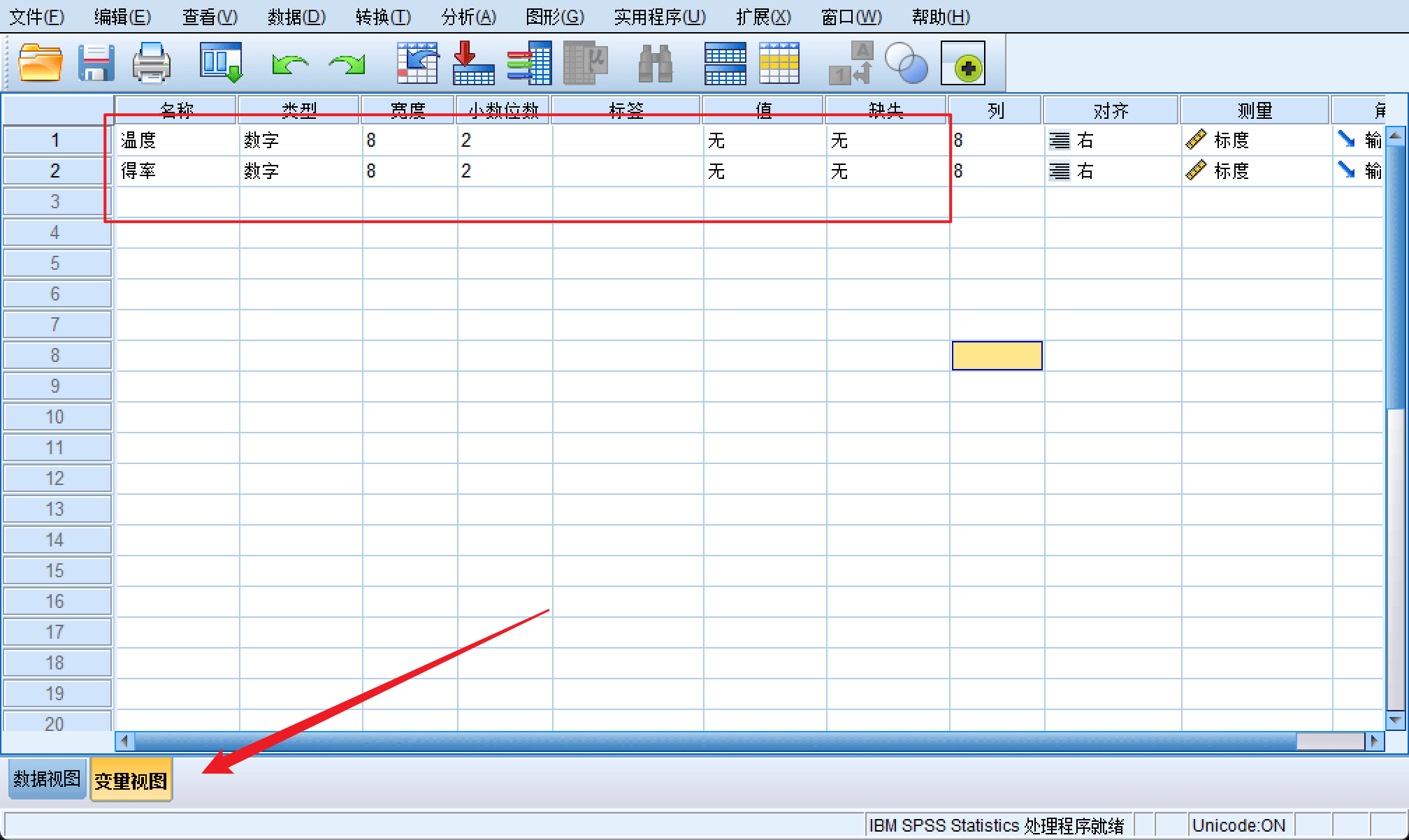
输入数据:
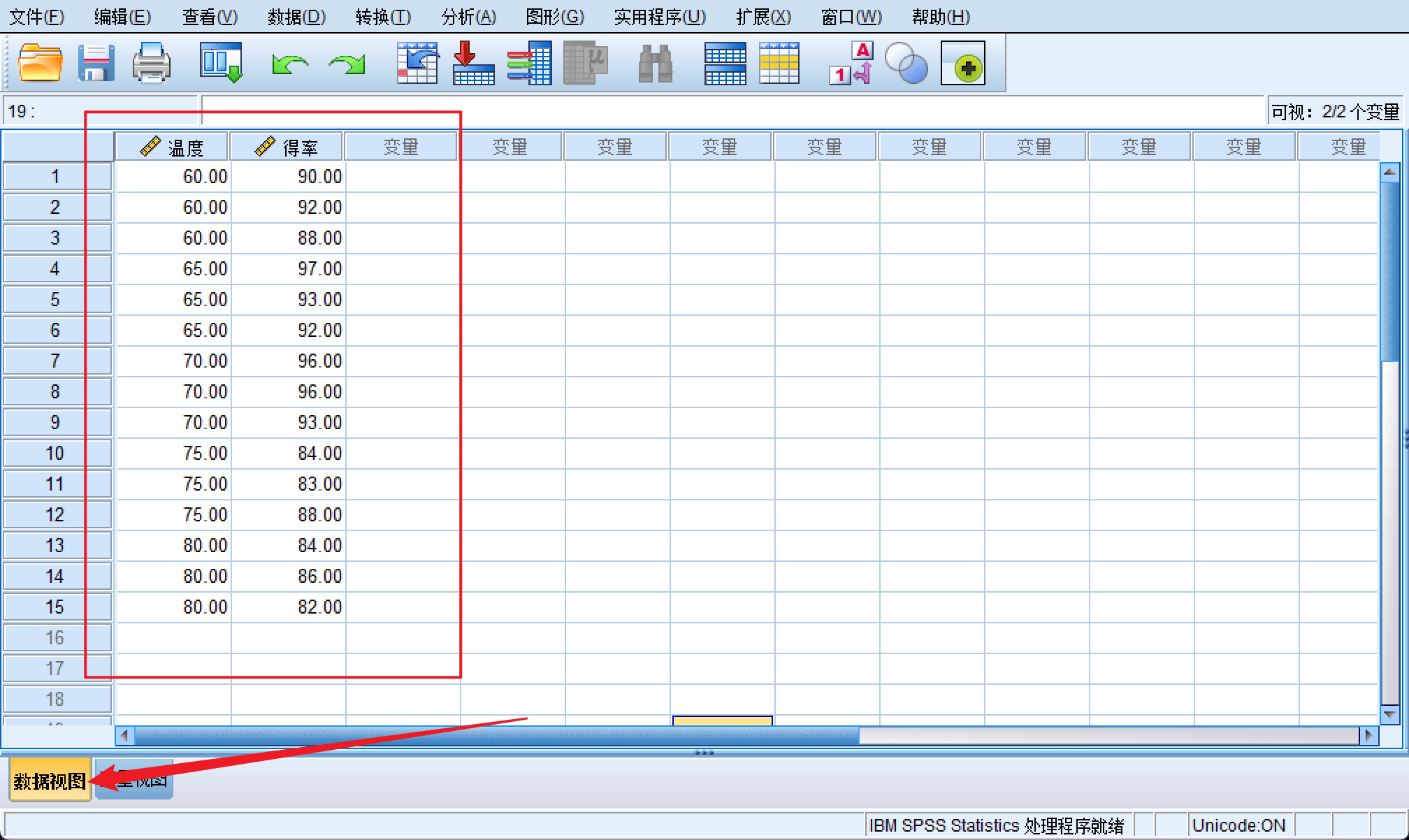
2.3 进行单因素方差分析
选择分析-> 比较平均值->单因素ANOVA检验:
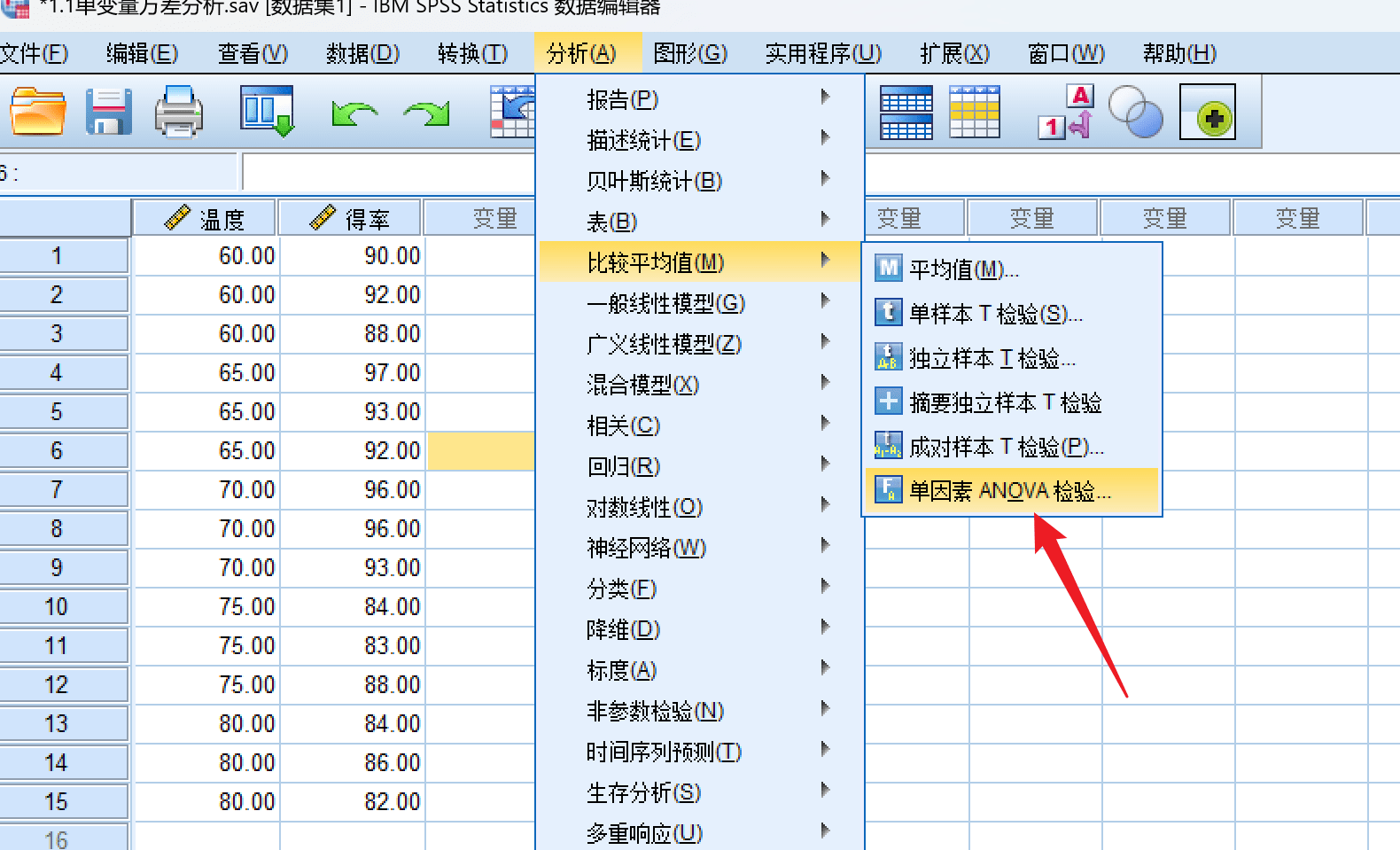
选定变量: 
得出下面的结果:
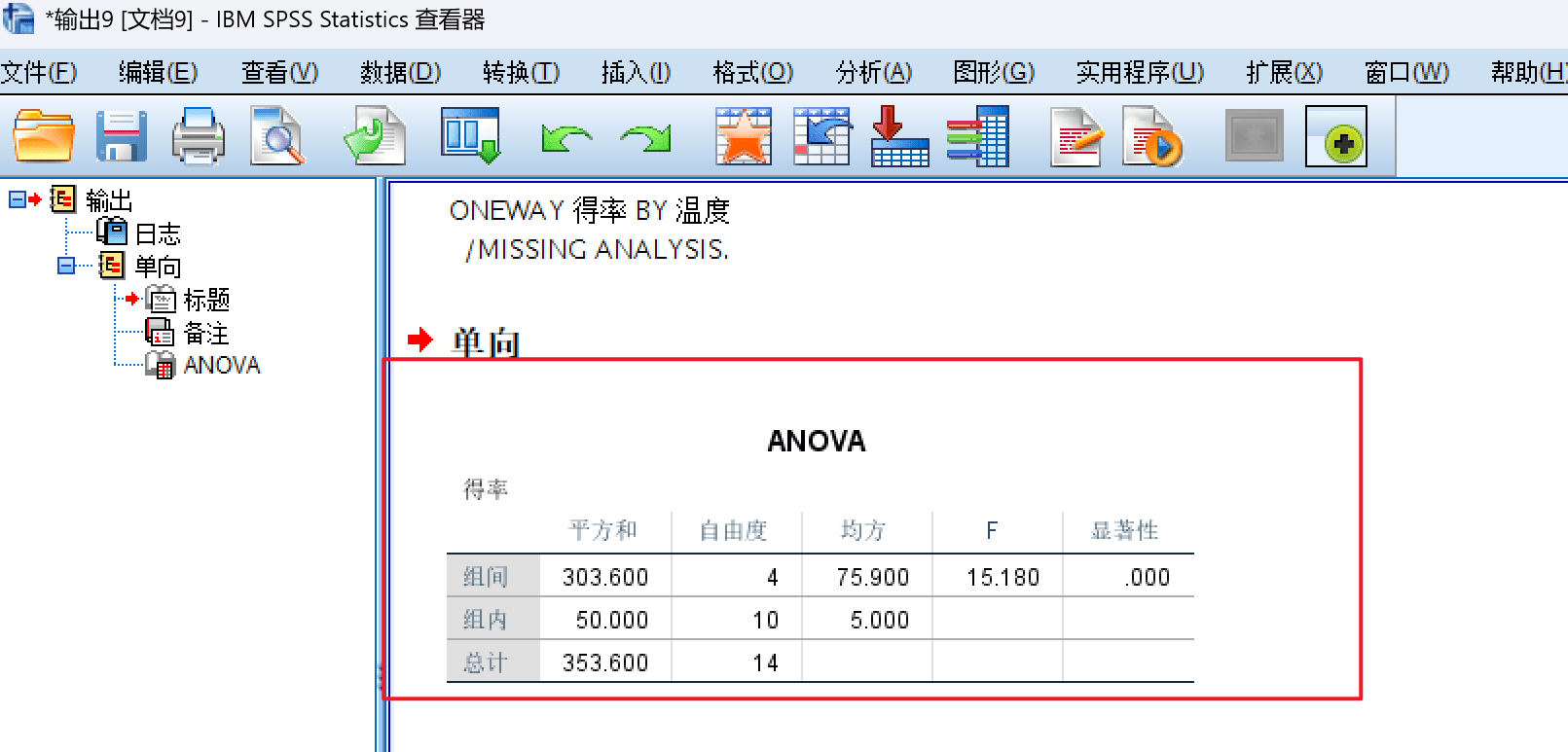
可以看到输出结果如下:
| 来源 | 平方和 | 自由度 | 均方 | F 值 | 显著性(p 值) |
|---|---|---|---|---|---|
| 组间(Between Groups) | 303.600 | 4 | 75.900 | 15.180 | .000 |
| 组内(Within Groups) | 50.000 | 10 | 5.000 | ||
| 总计(Total) | 353.600 | 14 |
三、双因素方差分析
在之前,我们讨论了单因素方差分析(One-Way ANOVA),它用于检验一个分类型自变量(因子)对一个连续型因变量的影响。
双因素方差分析(Two-Way ANOVA)则更进了一步,它允许我们同时研究两个分类型自变量(因子)如何影响一个连续型因变量。
举个例子:
- 单因素:研究“不同肥料”(因子A)对“作物产量”(因变量)的影响。
- 双因素:同时研究“不同肥料”(因子A)和“不同光照时长”(因子B)对“作物产量”(因变量)的影响。
使用双因素方差分析,我们不仅可以分别检验每个因子(肥料、光照)的主效应 (Main Effect),更重要的是,我们还可能(取决于实验设计)检验两个因子之间的交互作用 (Interaction Effect)。
“交互作用”是一个非常关键的概念。它指的是:一个因子的效果,是否会因为另一个因子的不同水平而发生改变?
交互作用示例:
- 无交互:无论光照是长是短,A肥料总是比B肥料增产10公斤。
- 有交互:在“长光照”下,A肥料效果最好;但在“短光照”下,B肥料的效果反而逆转,变得最好。
根据实验设计在每个“单元格”(即两个因子的特定组合)中是只有一个观测值还是有多个观测值,双因素方差分析分为两种类型:无重复和可重复。
3.1 无重复双因素方差分析
1. 介绍
无重复双因素方差分析,也称为“无交互作用的双因素方差分析”或“随机区组设计”
在这种设计中,对于两个因子(如 因子A 和 因子B)的每一种水平组合(也称为一个 "单元格" 或 "处理"),你只有一个观测值。
数据表示例: 假设研究 3 种不同肥料(因子A)和 2 种不同光照(因子B)对产量的影响。你的数据表看起来像这样,每个单元格只有 1 个数据:
| 因子A / 因子B | 光照长 | 光照短 |
|---|---|---|
| 肥料甲 | 产量 1 (25kg) | 产量 2 (18kg) |
| 肥料乙 | 产量 3 (28kg) | 产量 4 (20kg) |
| 肥料丙 | 产量 5 (22kg) | 产量 6 (15kg) |
| 由于每个组合只有一个数据点,我们无法区分“交互作用”和“随机误差”。因此,这种模型的核心假设是:因子A 和 因子B 之间不存在交互作用。 |
在这种假设下,我们分析的目标是:
- 检验 因子A (肥料) 的主效应:不同肥料对产量有无显著影响?
- 检验 因子B (光照) 的主效应:不同光照时长对产量有无显著影响?
2. SPSS实战
这里的数据来自于《实验设计与数据分析—李云雁(第三版)》-P99
| pH值 / 硫酸铜浓度 | B1 | B2 | B3 |
|---|---|---|---|
| A1 | 3.5 | 2.3 | 2.0 |
| A2 | 2.6 | 2.0 | 1.9 |
| A3 | 1.4 | 0.8 | 0.3 |
| A4 | 1.4 | 0.8 | 0.3 |
将数据输入SPSS:
定义变量: 
输入数据:
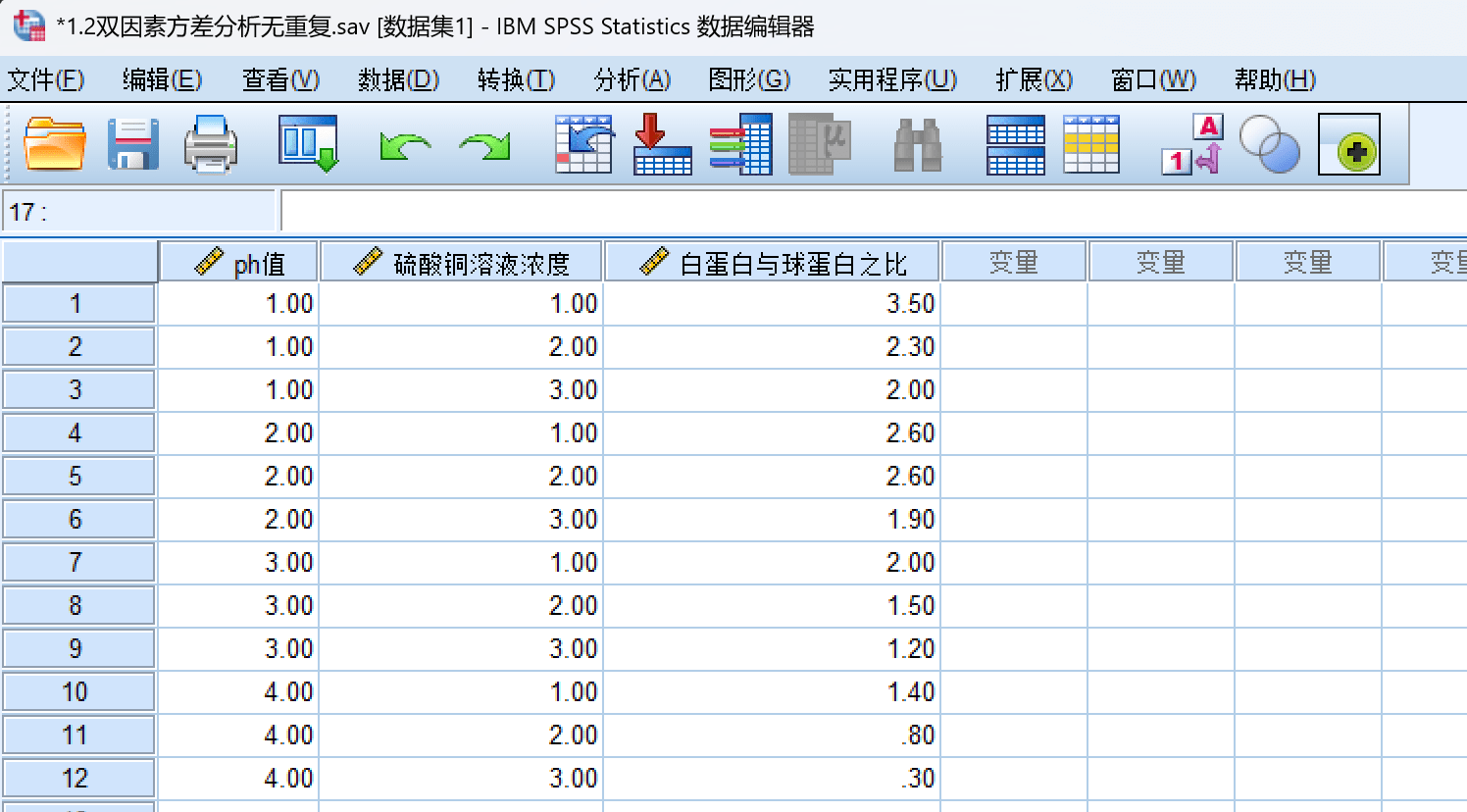
注意这里的Ph 和硫酸铜浓度写 1、2、3和1、2、3、4并不是真实值 ,只是指代某一水平而已
进行单变量分析:
模型如下:
最终得到分析结果:
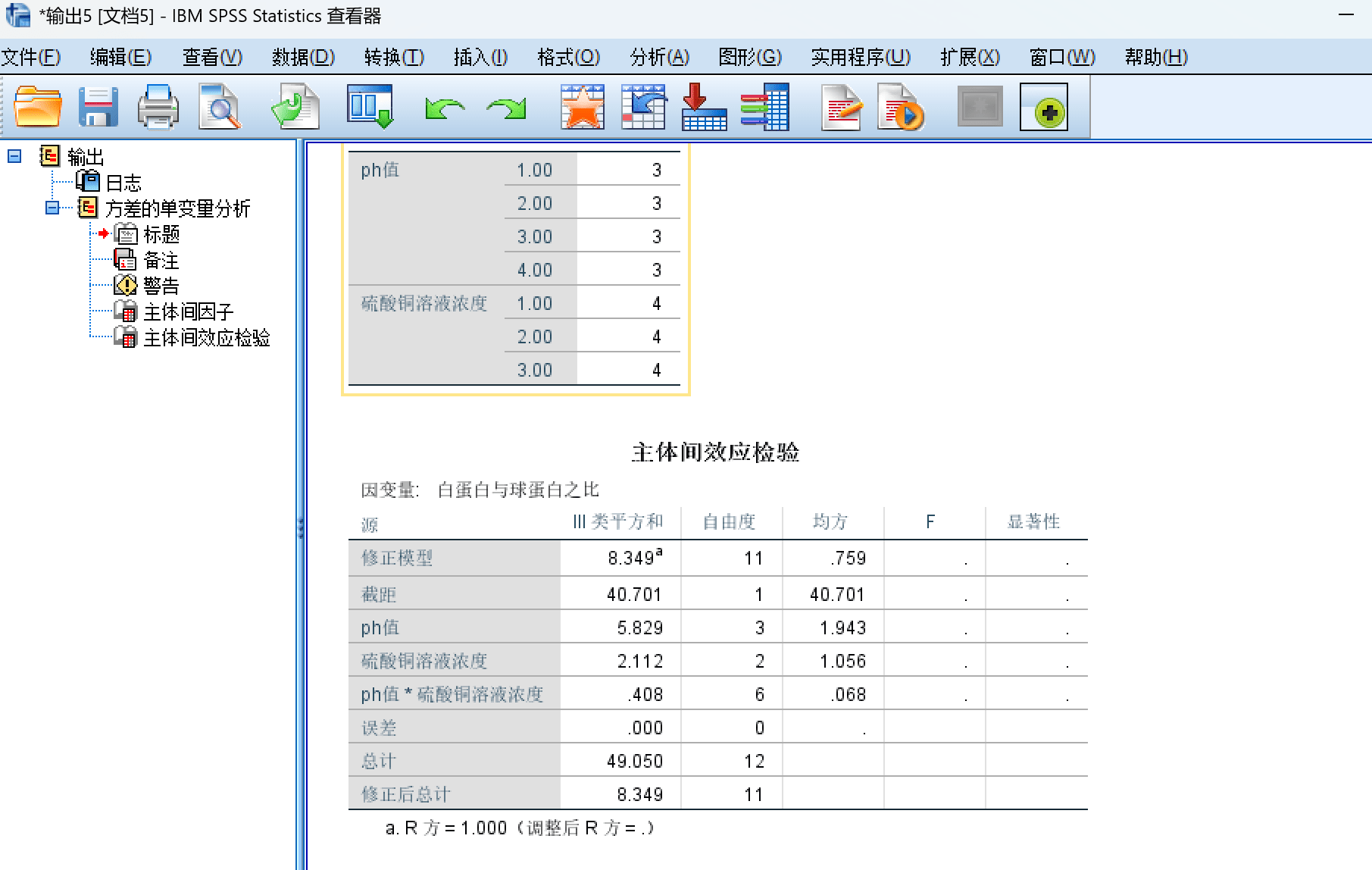
3.1 可重复双因素方差分析
1. 介绍
这是功能更强大、应用更广泛的一种模型。在这种设计中,对于两个因子的每一种水平组合(每个 "单元格"),你有多个(n > 1)观测值。数据表示例: 同样是上面的例子,但这次,每种处理组合下,你都种了 3 块实验田(即 n=3):
| 因子A / 因子B | 光照长 | 光照短 |
|---|---|---|
| 肥料甲 | 25kg, 26kg, 24kg | 18kg, 19kg, 17kg |
| 肥料乙 | 28kg, 29kg, 27kg | 20kg, 21kg, 22kg |
| 肥料丙 | 22kg, 21kg, 23kg | 15kg, 16kg, 14kg |
| 由于在同一个单元格(例如 "肥料甲" + "光照长")内有了多个观测值(25, 26, 24),我们就可以计算出这个单元格内部的变异。这种 "单元格内部" 的变异被认为是纯粹的随机误差 (Within-group Error)。 |
这使得我们能够将总变异分解得更精细,从而检验交互作用!
分析的目标是:
- 检验 因子A (肥料) 的主效应。
- 检验 因子B (光照) 的主效应。
- 检验 因子A 和 因子B 之间的交互作用。
2. SPSS实战
这里的数据来自于《实验设计与数据分析—李云雁(第三版)》-P101,数据如下
| 浓度 / 温度 | 10℃ | 24℃ | 38℃ | 52℃ |
|---|---|---|---|---|
| 2 | 14, 10 | 11, 11 | 13, 9 | 10, 12 |
| 4 | 9, 7 | 10, 8 | 7, 11 | 6, 10 |
| 6 | 5, 11 | 13, 14 | 12, 13 | 14, 10 |
| 输入到SPSS: |
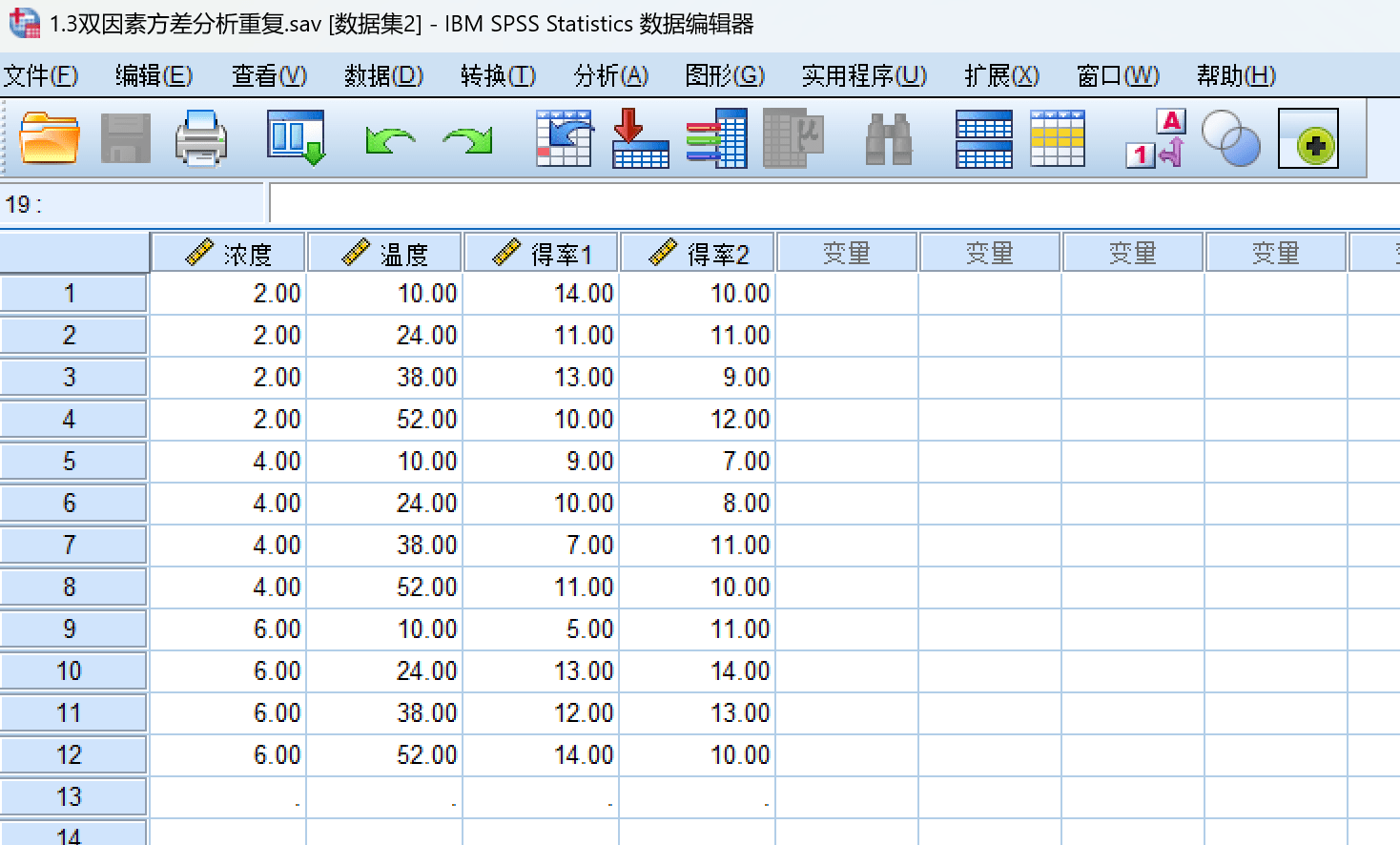
进行重复分析:
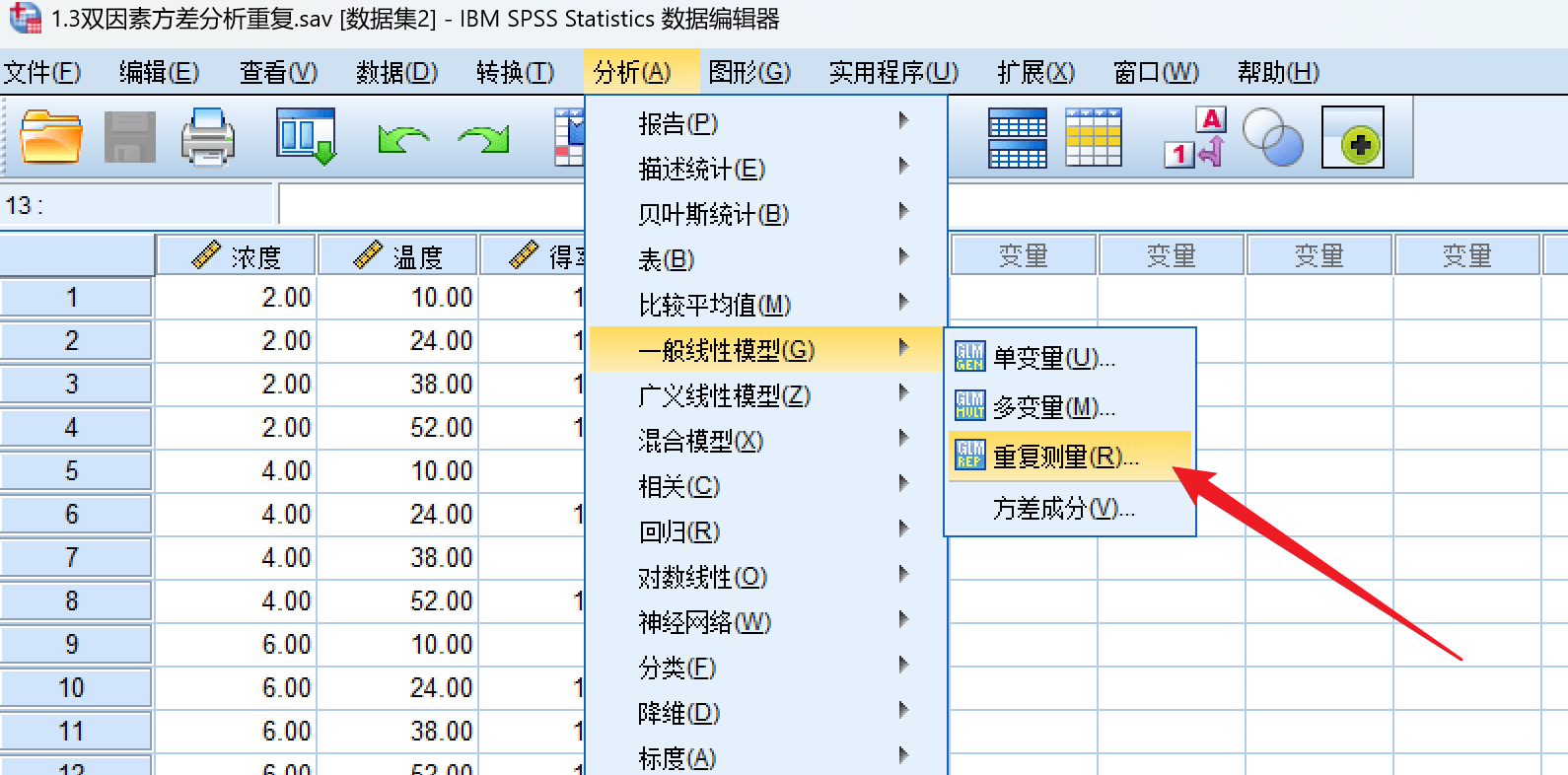
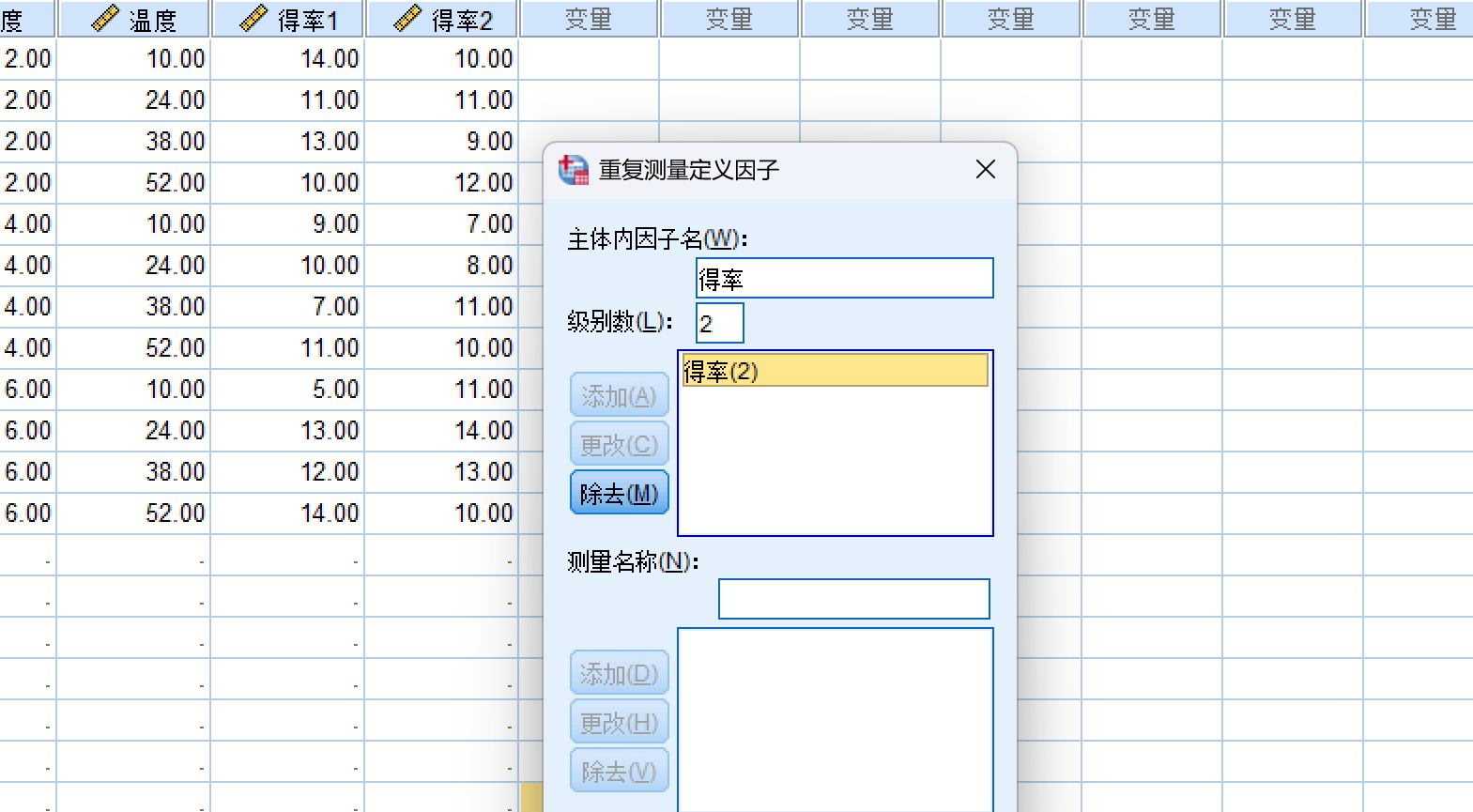
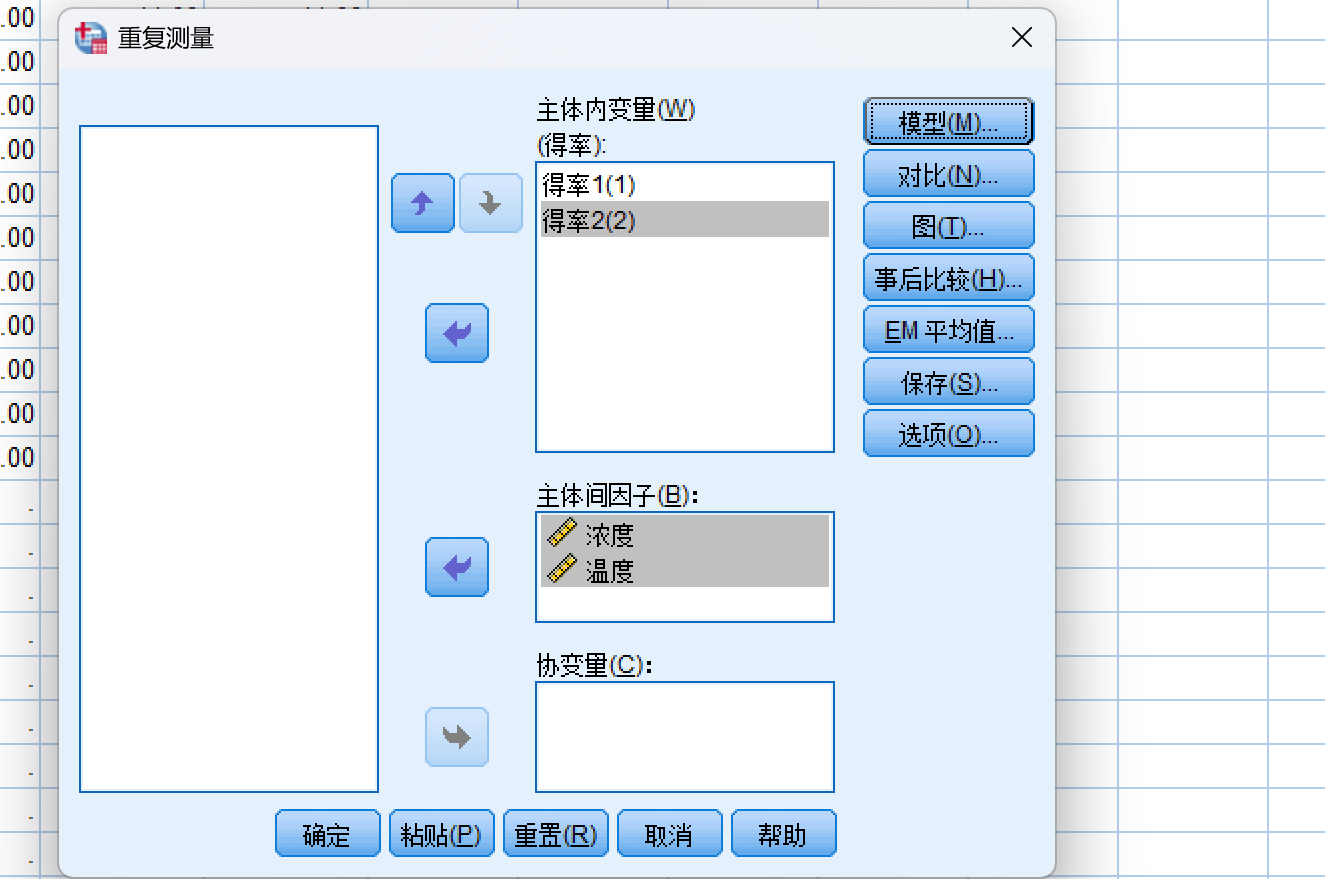
分析得到结果: