SPSS回归分析

在实验设计与数据分析中，我们常常会遇到“多个因素共同影响结果”的情况。为了揭示这些因素与结果之间的关系，回归分析（Regression Analysis） 成为最常用的统计工具之一。 它不仅能定量描述自变量（因素）与因变量（结果）之间的依赖关系，还能用于预测、优化与显著性判断。

而 SPSS（Power Analysis and Sample Size） 软件除了我们熟知的样本量估计与显著性分析功能外，其实也内置了功能强大的 线性回归分析模块，适合科研实验、工程分析、农业试验等领域的用户快速完成回归模型的建立与统计检验。

---

一、什么是回归分析？

回归分析的核心思想是：

通过拟合数学模型，描述一个或多个自变量对因变量的影响关系。

常见形式包括：

• 简单线性回归：一个自变量与一个因变量的线性关系；
• 多元线性回归：多个自变量共同影响一个因变量；
• 非线性回归：变量关系不是线性的（如指数、对数、多项式等）；
• 回归诊断：用于检验模型的拟合优度、显著性和残差特性。

回归方程的一般形式如下：

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_n{X}_n+\epsilon$$

其中：

• $Y$：因变量（结果变量）
• $X_i$：自变量（影响因素）
• ${\beta }_i$：回归系数（影响程度）
• $\epsilon$：随机误差项

---

二、一元线性回归

一元线性回归用于分析 单个自变量 与因变量之间的线性关系，其回归方程为：

$$Y={\beta }_0+{\beta }_{1}X+\epsilon$$

• $Y$：因变量（结果）
• $X$：自变量（影响因素）
• ${\beta }_0$：截距
• ${\beta }_1$：斜率（每单位自变量变化对因变量的影响）
• $\epsilon$：随机误差项

SPSS 中一元线性回归的操作：

输入数据：

这里我们使用课本上的示例数据：《实验设计与数据分析—李云雁（第三版）》-P106

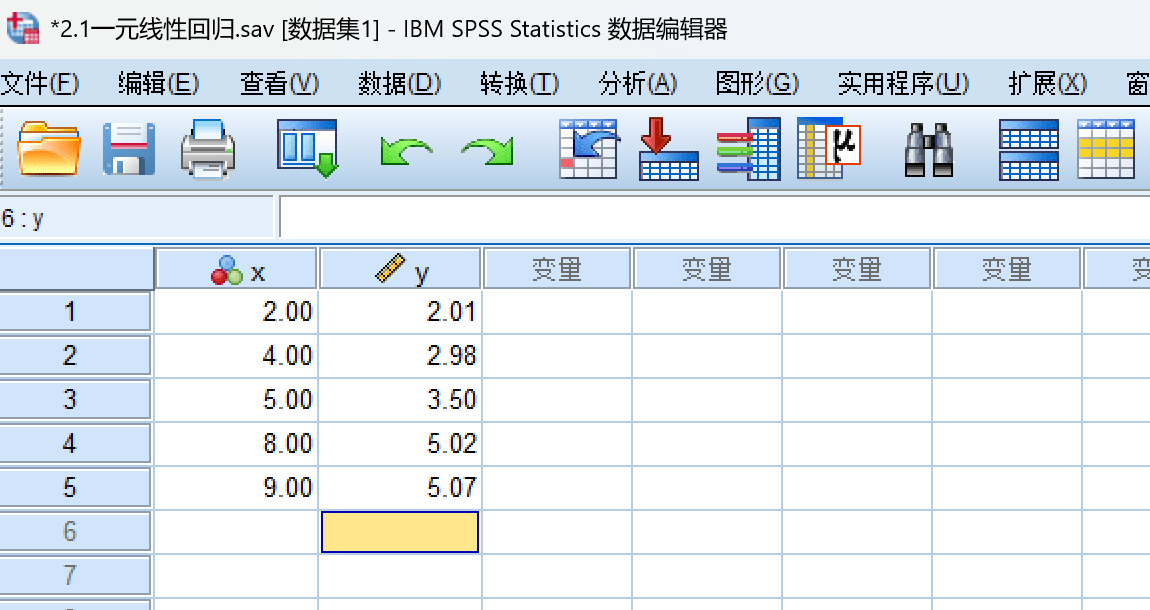
进行分析：

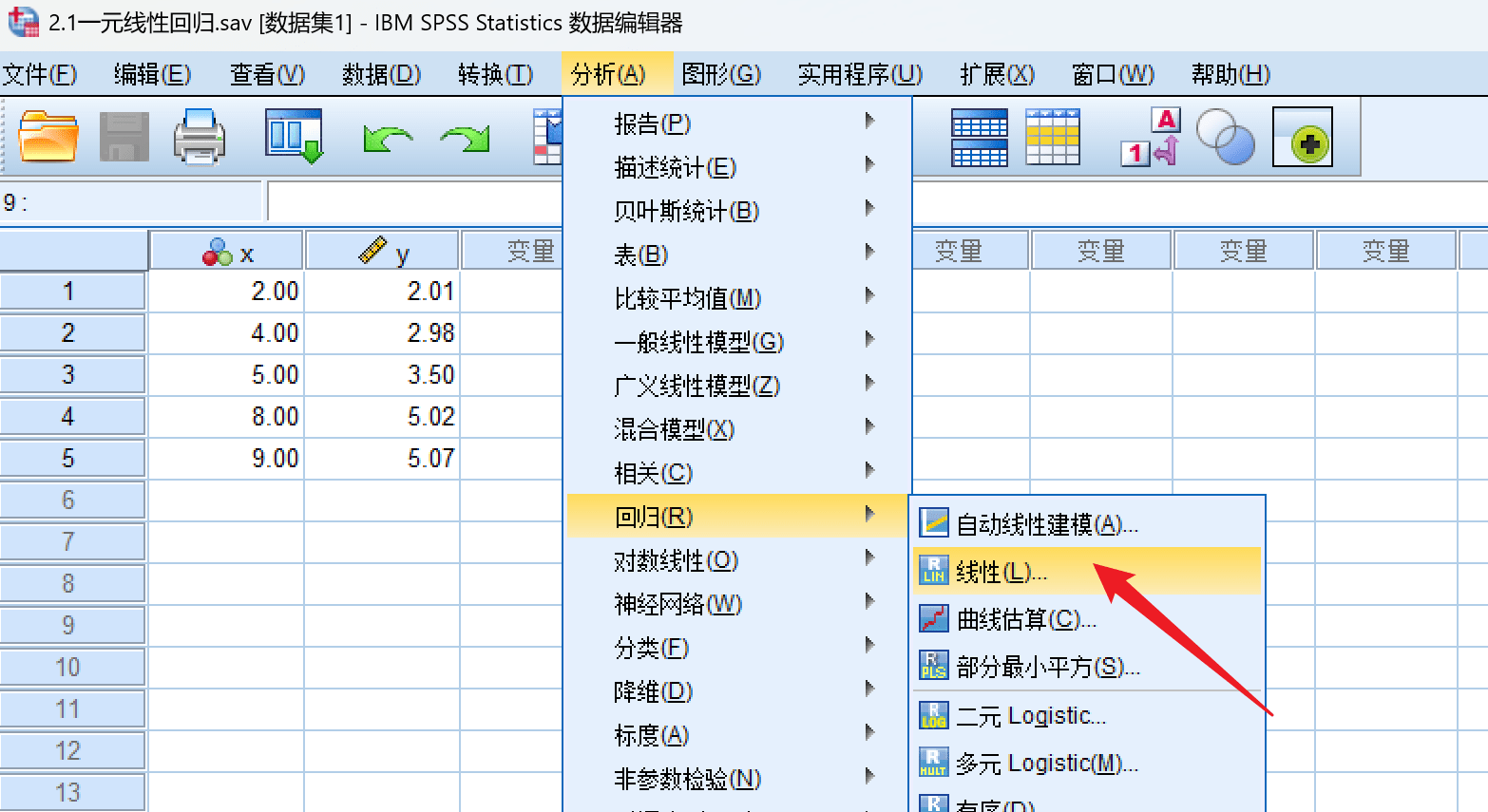
选好自变量和因变量：

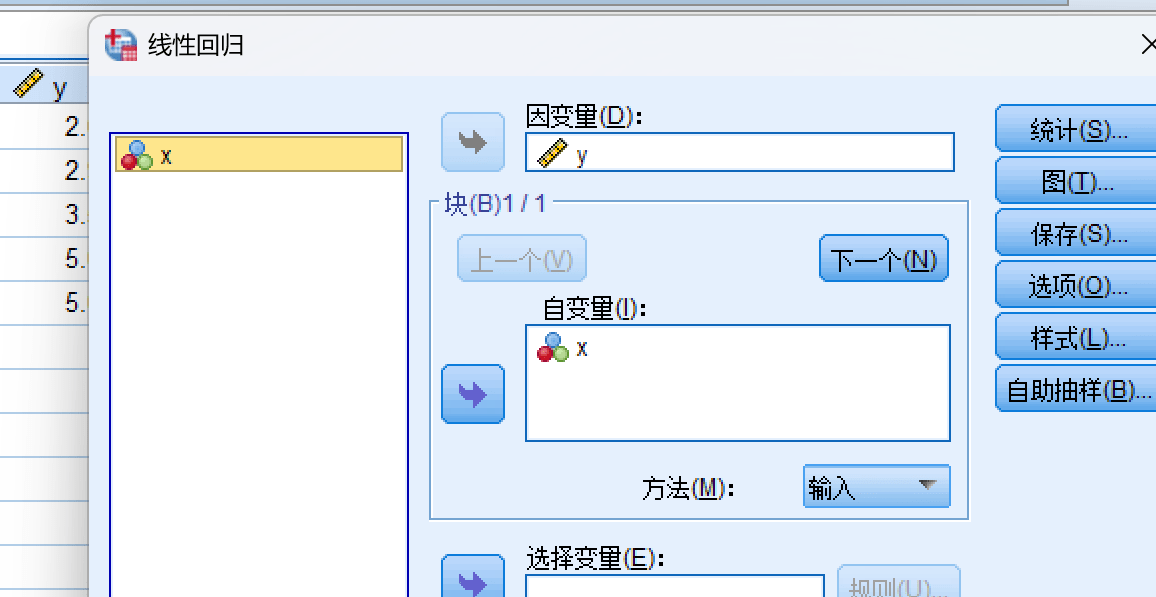
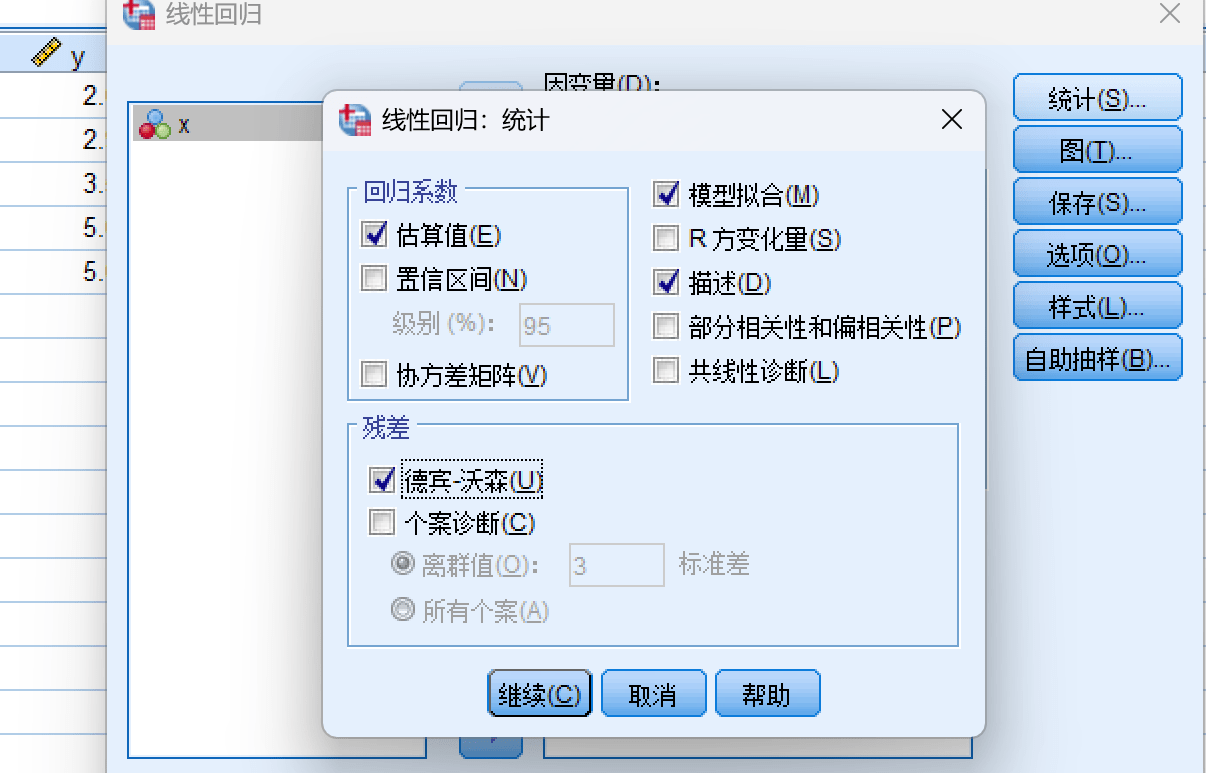
结果如下：

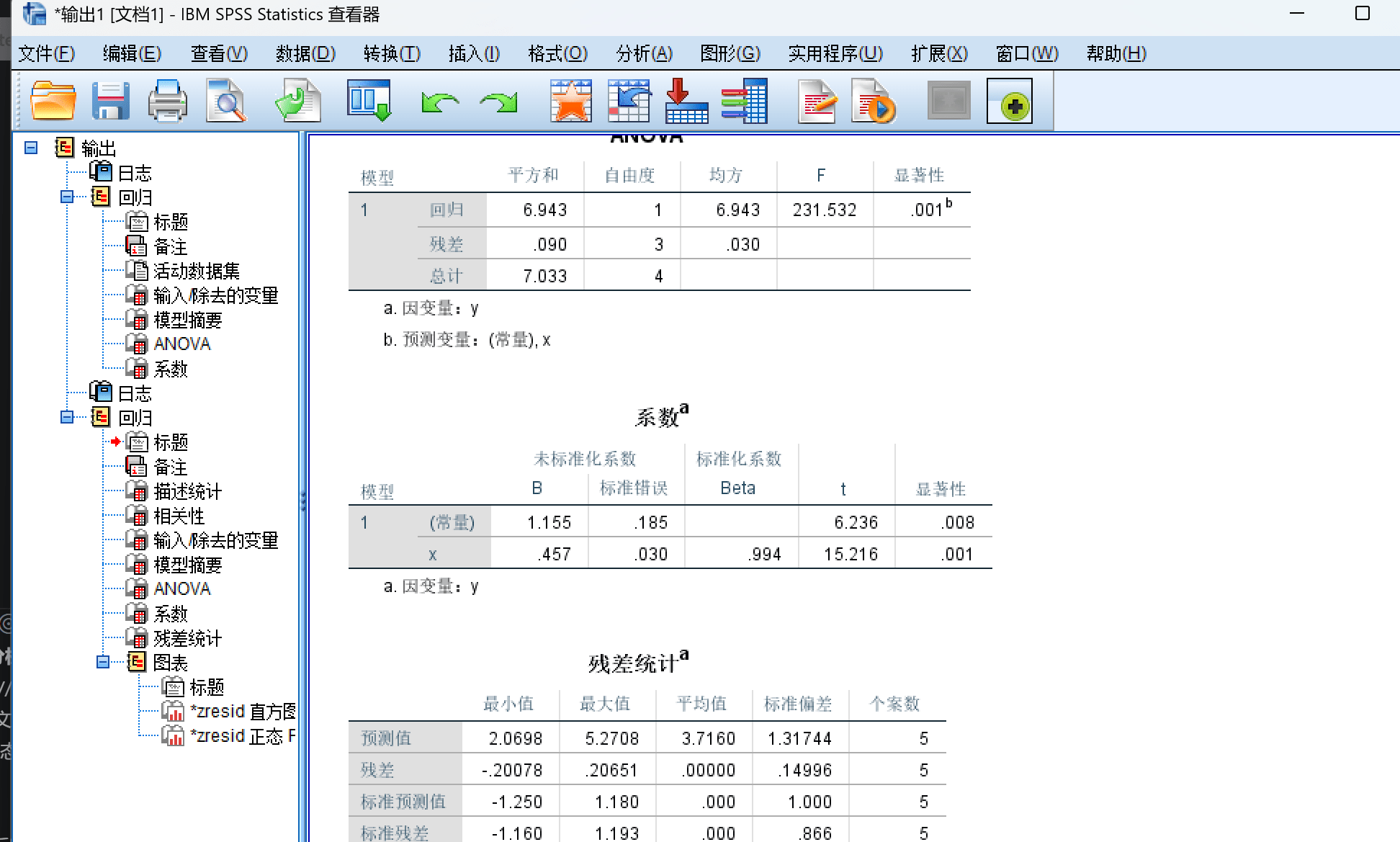
可以看到计算的系数为1.115 和 0.4573 和书上一致

---

三、多元线性回归

多元线性回归用于分析 多个自变量 对一个因变量的联合影响，其回归方程为：

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_n{X}_n+\epsilon$$

• $X_1,X_2,\dots ,X_n$：多个自变量
• ${\beta }_i$：对应自变量的回归系数
• 其他符号同一元回归

使用SPSS处理方法与一元基本一致，这里不再展示。

结果解读要点：

• 整体显著性：F 检验 p 值 < 0.05 → 整体模型显著；
• 单因素显著性：各回归系数 t 检验 p 值 < 0.05 → 该自变量对因变量显著；
• 拟合优度：调整后的 $R^2$ 可衡量模型解释力，考虑自变量数量的影响；
• 多重共线性：VIF > 10 提示变量间可能存在共线性问题，需要剔除或合并变量。

多元回归能够同时考虑多个因素的影响，常用于实验优化、预测模型建立以及因素排序。

---